Tworzenie wykresów naukowych za pomocą GLE, cz. 2

Czas na błędy

Załóżmy, że mamy dane eksperymentalne zapisane w pliku daneexp.dat w ten sposób, że pierwsza kolumna odpowiada „x-om'', druga kolumna wartościom zmierzomym czyli „y-om'', zaś w trzeciej kolumnie znajdują się wartości błędów eksperymentalnych. Stwórzmy więc kod wykresu

size 20 10
set hei .8
set font texcmr
begin graph
xtitle "Iksy"
ytitle "Igreki"
xaxis min 0 max 3 dticks 1 hei .5
yaxis min 0 max 6 dticks 1 hei .5
data daneexp.dat d1=c1,c2 d2=c1,c3
d1 marker square msize 0.3 color blue err d2
end graph

który po skompilowaniu będzie wyglądał tak:

Rysunek 5. Wykres z błędami eksperymentalnymi.

Jak widać w kodzie zdefiniowaliśmy dwie serie danych: serię d1 oraz serię d2. Następnie wykreślamy serię d1 w postaci punktów oznaczonych kwadratami, zaś serię d2 uznajemy za wartości błędów i dołączamy do serii d1 za pomocą polecenia err. Dostaliśmy więc wykres wraz ze słupkami błędów. Możliwe jest także definiowanie oddzielnie słupków błędów górnych i dolnych. Służą do tego polecenia, odpowiednio, errup oraz errdown. Możliwe jest także zdefiniowanie błędów eksperymentalnych jako wielkości stałej lub proporcjonalnej do wielkości zmierzonej. W pierwszyp przypadku zapisujemy to tak:

d1 marker wsquare err 0.5

co oznacza, że wilkość błędu zawsze będzie wynosić 0.5, zaś w drugim przypadku np. tak:

d1 marker wcircle errup 15% errdown 20%

co oznacza, że wielkość błędu górnego wynosi 15% wartości zmierzonej, zaś wielkość błędu dolnego wynosi 20% wartości zmierzonej.
Istnieje także polecenie herr które pozwala pokazać poziome słupki błędów (oraz analogiczne polecenia herrup i herrdown).

Więcej o poleceniu key

Dotychczas używaliśmy polecenia key w dość trywialny sposób - gdy GLE pobierał dane do opisu serii danych z pliku. Polecenie key ma jednak wiele więcej możliwości. Poprawmy więc nasz kod

size 20 10
set hei .8
set font texcmr
begin graph
key pos tl compact nobox hei .4 offset 0.5 0.5
xtitle "Iksy"
ytitle "Igreki"
xaxis min 0 max 3 dticks 1 hei .5
yaxis min 0 max 6 dticks 1 hei .5
data daneexp.dat d1=c1,c2 d2=c1,c3 d3=c1,c4 d4=c1,c5
d1 marker square msize 0.3 color blue err d2
d3 marker square msize 0.3 color red err d4
d1 key "To są dane eksperymentalne nr 1"
d3 key "To są dane eksperymentalne nr 2"
end graph

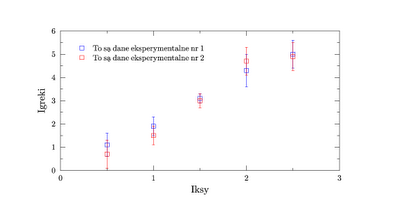
który po skompilowaniu będzie wyglądał tak:

Rysunek 6. Wykres z błędami eksperymentalnymi - wersja poprawiona.

W linii piątej dodaliśmy za pomocą komendy key polecenie utworzenia legendy. Dodaliśmy także drugą serię danych (z błędami). Natomiast w liniach trzynastej i czternastej zdefiniowaliśmy wprost opis naszych serii danych w legendzie wykresu.


W przypadku bardziej skomplikowanych podpisów można używać modułu key oddzielnie, a nie wewnątrz modułu graph. Na przykład z powyższego przykładu usuńmy linie: 5, 13 i 14, zaś moduł key zdefiniujmy oddzielnie:

size 20 10
set hei .8
set font texcmr
begin graph
xtitle "Iksy"
ytitle "Igreki"
xaxis min 0 max 3 dticks 1 hei .5
yaxis min 0 max 6 dticks 1 hei .5
data daneexp.dat d1=c1,c2 d2=c1,c3 d3=c1,c4 d4=c1,c5
d1 marker square msize 0.3 color blue err d2
d3 marker square msize 0.3 color red err d4
end graph

begin key
pos tl offset 0.5 0.5 nobox compact hei 0.4
text "Dane eksperymentalne"
marker square msize 0.3 color blue text "Seria nr 1"
text "(Eksperyment nr 1 z dnia 01.01.2009)"
marker square msize 0.3 color red text "Seria nr 2"
text "(Dane z pracy [1])"
end key

Po skompilowaniu powinniśmy otrzymać coś takiego:

Rysunek 7. Wykres z błędami eksperymentalnymi - wersja ostatnia.

Polecenie let

Polecenie let umożliwia nam ustawienie wartości danej serii w postaci funkcji analitycznej. Ogólna postać tego polecenia to:

let dx = wyrażenie from kres_dolny to kres_górny step krok

przy czym parametry from, to oraz step są opcjonalne. Na przykład

let d1 = sin(x) from 0.0 to 10.0 step 0.1

zapełnia nam serię danych d1 wartościami six(x) dla x od 0 do 10 zmieniającymi się co 0.1. Oczywiście tak stworzoną serię danych mozemy zamieścić na wykresie. Polecenie let przydaje się gdy nasze dane eksperymentalne chcemy porównać z jakąś prostą funkcją analityczną.

Manipulacja danymi - manip

Spójrzmy na następujący przykład:

size 20 12
set hei .8
set font texcmr
begin graph
xtitle "Energy [eV]"
ytitle "Intensity (arbitrary scale)"
xaxis min 6640 max 6690 dticks 10 hei .5
yaxis min 0 max 1.1 dticks 0.2 hei .5
data fe.s d1=c1,c2
data fe.sx d2=c1,c2
d1 impulses color blue
d2 line color red
end graph
amove 12 7
text Fe K\alpha_1_,_2

Po skompilowaniu otrzymamy wykres taki jak na Rys. 8. Rysunek zawiera wykres słupkowy oraz wykres zobrazowany linią ciągłą. Wszystko byłoby dobrze, gdyby niebieskie słupki nie wychodziły poza czerwoną linię - gdyż nie jest to zbyt eleganckie. Możemy temu zaradzić używajac dołączonego do GLE programu manip.

Rysunek 8. Wykres widma.

Wpisujemy zatem w powłoce systemowej polecenie:

manip fe.s

(z niewadomych dla mnie powodów manip na problem z wczytywaniem plików z wielkimi literami w nazwie). Powinniśmy ujrzeć widok, jak na Rys. 9.

Rysunek 9. Program manip w akcji.

Program manip, zgodnie z nazwą, służy do manipulacji danymi. W naszym przypadku użyjemy go, aby zmniejszyć wartości znajdujące się w drugiej kolumnie pliku fe.s do połowy swojej wartości. Będąc już w manip-ie wpisujemy

c2=c2*0.5

co oczywiście zamieni nam wartości drugiej kolumny pliku na te same wartości, ale pomnożone przez 0.5. Po następnym skompilowaniu naszego obrazka w GLE powinniśmy otrzymać wykres taki jak na Rys. 10.

Rysunek 10. Poprawiony wykres widma.

Według mnie wykres wygląda teraz estetyczniej. Oczywiście nie musimy nadpisywać drugiej kolumny pliku fe.s - z doświadczenia wiem, że często warto zachowywać orginalne dane. Będąc w manip-ie mozemy zatem wydać polecenie

c4=c2*0.5

co wypełni nam kolumnę czwartą (to nic, że wcześniej jej nie było) wartościami z drugiej kolumny pomnożonymi przez 0.5. Wystarczy teraz tylko w pliku .gle zamienić linię kodu

data fe.s d1=c1,c2

na linię

data fe.s d1=c1,c4

i po skompilowaniu znów zobaczymy wykres taki jak na Rys. 10.


Oczywiście program manip potrafi o wiele więcej (kopiowanie, przenoszenie, sortowanie, usuwanie, generowanie i sumowanie danych w kolumnach), ale nie o nim miałem się w tym artykule rozpisywać.

Słowo na zakończenie

GLE jest potężnym programem, a to co opisałem w niniejszym artykule stanowi tylko ułamej jego możliwości. Wiele ciekawych efektów, takich jak wiele obszarów wykresy na jednym obrazku czy też obszar wykresu w obszarze wykresu, da się osiągnąc za pomocą poleceń amove i rmove. GLE dobrze też sobie radzi z wykresami trójwymiarowymi, ale to już jest temat na oddzielny artykuł.

Mam natomiast nadzieję, że ten artykuł przybliżył trochę program GLE - oczywiście tym którzy do tej pory go nie znali.

Odnośniki

http:glx.sourceforge.net/ - Strona główna projektu. Tamże można także znaleść podręcznik użytkownika (a nawet dwa)